Cryptographic Reverse Firewall via Malleable Smooth Projective Hash Functions
 Oblivious Transfer with CRFs
Oblivious Transfer with CRFs
Abstract
Motivated by the revelations of Edward Snowden, post- Snowden cryptography has become a prominent research direction in recent years. In Eurocrypt 2015, Mironov and Stephens-Davidowitz proposed a novel concept named cryptographic reverse firewall (CRF) which can resist exfiltration of secret information from an arbitrarily compromised machine. In this work, we continue this line of research and present generic CRF constructions for several widely used cryptographic protocols based on a new notion named malleable smooth projective hash function. Our contributions can be summarized as follows.
- We introduce the notion of malleable smooth projective hash function, which is an extension of the smooth projective hash function (SPHF) introduced by Cramer and Shoup (Eurocrypt’02) with the new properties of key malleability and element rerandomizability. We demonstrate the feasibility of our new notion using graded rings proposed by Benhamouda et al. (Crypto’13), and present an instantiation from the k-linear assumption.
- We show how to generically construct CRFs via malleable SPHFs in a modular way for some widely used cryptographic protocols. Specifically, we propose generic constructions of CRFs for the unkeyed message-transmission protocol and the oblivious signature-based envelope (OSBE) protocol of Blazy, Pointcheval and Vergnaud (TCC’12). We also present a new malleable SPHF from the linear encryption of valid signatures for instantiating the OSBE protocol with CRFs.
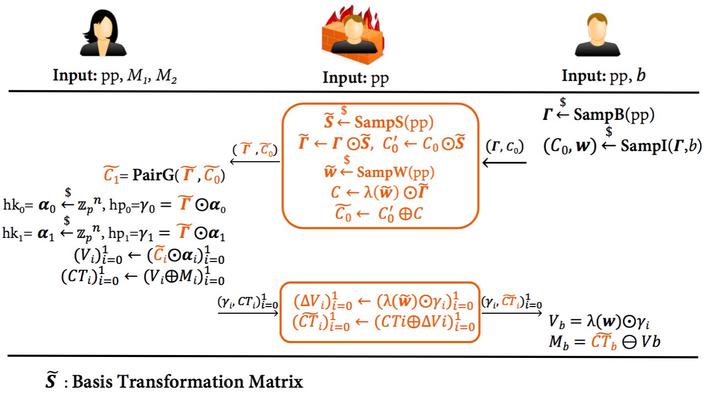
- We further study the two-pass oblivious transfer (OT) protocol and show that the malleable SPHF does not suffice for its CRF constructions. We then develop a new OT framework from graded rings and show how to construct OT-CRFs by modifying the malleable SPHF framework. This new framework encompasses the DDH-based OT-CRF constructions proposed by Mironov and Stephens-Davidowitz (Eurocrypt’ 15), and yields a new construction under the k-linear assumption.
Type
Publication
In 22nd Annual International Conference on the Theory and Applications of Cryptology and Information Security